Вернуться к оглавлению

 

15.2 Визуализация струнного заряда

В классическом Максвелловском электромагнетизме есть много различных конфигураций заряда: точечные частицы, линейные заряды, поверхностные заряды, и непрерывные распределения заряда. Т.к. мы уже видели, что струнный заряд локализован на струне, вы можете подумать, что струнная зарядовая плотность представляет собой что-то вроде некоторой линейной плотности Максвелловского заряда на струне. В действительности, это не так. Плотность заряда струны можно  представить, как Максвелловский ток на струне. Действительно, мы видели, что плотность заряда струны представляет собой пространственный вектор, направленный вдоль струны - в точности также, как выглядит Максвелловский ток на струне.

Плотность заряда струныможно проинтегрировать по всему пространству; при этом мы получаем общий заряд струны (15.20). Этот заряд имеет некоторые недостатки: он является бесконечным для струны бесконечной длины (см.(15.27)), и он пропадает для стягиваемой замкнутой струны (Задача 15.3). Однако, возможно использовать плотность струнного заряда для вычисления количества струн. Число струн N, определенное ниже, определяет число струн, связанных заданным пространством.

Плотность заряда струны  ведет себя подобно электрическому току Максвелла вследствие (15.19). Сохранение электрического заряда в электромагнетизме требует

                                                                                              (15.29)

В магнитостатике плотность электрического заряда ρ не зависит от времени и, в результате, для плотности электрического тока дивергенция равна нулю. Это означает, что заряд не накапливается нигде и никогда. Бездивергентные токи не могут остановиться. Когда они текут по проводам либо провода формируют циклы (для нас это замкнутые струны), либо они бесконечно длинные (бесконечные струны). Мы знаем, что  даже тогда, когда мы имеем конфигурацию струны, зависящую от времени. Такая электрическая плотность заряда струны во всем аналогична электрическому току в магнитостатике. Сохранение струнного заряда требует, чтобы струны формировали замкнутые циклы или были бы бесконечно длинными.

Чтобы использовать и далее аналогию с магнитостатикой, мы изучим поля Калб-Рамона, созданные статическими струнами. Мы увидим, что величина напряжения поля Калб-Рамона может быть закодирована эффективным магнитном полем. Для упрощения выкладок мы будем работаем в четырех-мерном пространстве-времени. Имеются две возможности относительно уравнения (15.14): либо оба свободных индекса являются пространственными, либо один из них - временной, а другой - пространственный. В первом случае мы имеем

 ,                                                                                              (15.30)

т.к. j^ik пропадает для статических струн. Мы удовлетворим этому уравнению следующим условием: все компоненты H не зависят от времени и

H^ijk = 0.                                                                                                   (15.31)

Другое рассматриваемое выражение есть

                                                                                         (15.32)

Мы представим это уравнение в форме Максвелловского уравнения, вводя вектор   с компонентами B_{H m}, определенными след. образом:

H^0kl = ε^klm B_{H m} .                                                                                      (15.33)

Здесь ε^ijk - полностью антисимметричен и удовлетворяет ε¹²³ = 1. Вектор    называется напряжением поля, дуальным к Н. Подставляя обратно в (15.32), мы находим

                                      (15.34)

Теперь релевантные компоненты H уже закодированы в дуальном “магнитном поле”, и уравнение (15.32) эквивалентно исходному уравнению для H; если мы не можем его решить, то нет решения и для H. Условие согласованности для (15.35) известно. Т.к. дивергенция ротора есть нуль, существование решения требует (еще раз), чтобы был бездивергентным. Альтернативно, задав замкнутую одномерную кривую Г, которая является границей двумерной поверхности S, интегральная форма уравнения (15.35) есть

                                                                      (15.36)

Говорят, что кривая Г связывает струну, если струна пересекает каждую поверхность с границей Г. Если струна оканчивается в некоторой точке, ток  также должен заканчиваться в этой точке, но тогда  не равно нулю, что приводит к несогласованности в (15.35). Если струна оканчивается в некоторой точке, то для любой фиксированной Г левая сторона в (15.36) хорошо определена, но правая сторона должна зависеть от выбора поверхности S. Это говорит о несовместимости.

Уравнение (15.36) естественно приводит к определению струнного числа N, анонсированного в начале этой секции. Струнное число N, ассоциированное с кривой Г, определено, как

                                                          (15.37)

Мы ожидаем, что N дает число струн, связанных кривой Г. Для иллюстрации этого давайте вычислим значение N для струны, расположенной вдоль оси х¹, которая рассматривалась в предыдущей секции. Мы предполагаем, однако, что есть только три пространственные размерности, поэтому применимы результаты настоящей раздела. Выбирая ориентацию так, чтобы f'(σ) > 0, уравнение (15.27) дает

j⁰¹ = ½δ(y) δ(z).                                                                                      (15.38)

Рассмотрите теперь замкнутую кривую Г связывающую струну и лежащую в плоскости постоянного х. Предположим, что на этой плоскости кривая ограничивает поверхность S, чья ориентированная нормаль указывает в положительном направлении х. Т.к. оба - и вектор нормали и указывают в направлении х, мы находим

                (15.39)

Как ожидалось, мы получили N = 1. Вообще говоря, N = числу струн, связанных выбранной кривой. Имеет значение ориентация: если кривая связывает две струны с противоположными ориентациями, то их индивидуальные вклады в N будут уничтожаться. Поле  в заданном выше примере может быть легко вычислено. Можно также записать явное выражение для антисимметричного тензорного поля (Задача 15.4).

Давайте сравним с электромагнетизмом. Для локализованного распределения Максвелловского заряда, заряд вычисляется путем интегрирования плотности электрического заряда по трехмерному шару B³, ограниченному подходящей двумерной поверхностью S², которая заключает в себе заряды (см. рис. 15.1). Набор параллельных бесконечных струн окружен, но не заключен, подходящей окружностью S¹. Это является естественной аналогией: также, как электрические заряды не прикасаются к поверхности S², которая их заключает, струны не прикасаются к "поверхности" S¹, которая их связывает. Вы не можете убрать Максвелловский заряд без прокалывания двумерной сферы и вы не можете убрать струну без рарушения петли. Вычисление, аналогичное объемному интегрированию от плотности Максвелловского заряда, дает число струн, связанных S¹, как интеграл от локального потока плотности заряда струны по двумерному шару В² (диску), чьей границей является S¹. Наконец, в Максвелловской теории, заряд может также быть вычислен, как потоковый интеграл электрического поля по поверхности S², которая заключает заряды. Струнное число вычисляется аналогично как интеграл от напряжения  вдоль кривой, которая связывает струны.

Быстрое вычисление 15.2 Струна лежит вдоль оси х¹ в мире с четырьмя пространственными размерностями х¹, х², х³, х⁴. Напишите пару уравнений, которые определяют сферу, которая связывает струну.

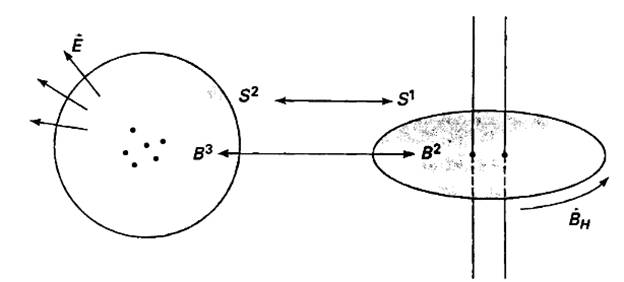
Рисунок 15. 1

Сравнение вычислений Максвелловского заряда и струнного числа в мире с тремя пространственными размерностями. Двумерная сфера, заключающая в себе Максвелловский заряд, аналогична окружности, связывающей струны.