Вернуться к оглавлению

 

15.1. Фундаментальный струнный заряд.

Как мы видели ранее, точечная частица может нести электрический заряд, потому что сущеструет взаимодействие, которое позволяет частице взаимодействовать с Максвелловским полем. Мировая линия точечной частицы - одномерная, а Максвеловское калибровочное поле несет один индекс. Это сооотвествие является очень важным. Траектория частицы имеет касательный вектор dx^μ(τ)/dτ, где τ параметризует мировую линию. Так как он имеет один Лоренцовский индекс, касательный вектор может быть умножен на калибровочное поле A_μ о образованием Лоренцовского скаляра. Работая с естественными единицами (ħ = с = 1), взаимодействие для точечной частицы заряда q, записанное, как член в действии, принимает форму

                                                                        (15.1)

Удобно потребовать безразмерность q в естественных единицах. Так как действие также является безразмерным в естесственных единицах, то калибровочное поле A_μ должно нести единицы обратной длины, или массы: [A_μ] = M. Напряженность поля имеет единицы [F_μν] = M², так как он получен дифференцированием калибровочного поля по пространственно-временным координатам.

Полная система взаимодействия заряженной частицы и Максвелловского поля определен действием, рассмотренным в Задаче 5.6:

                                            (15.2)

Первый член с правой стороны - это действие для частицы, а последний член - это действие для Максвелловского поля. Мы добавили безразмерную константу k₀ с единицами [k₀²] = M^D-4 с целью сделать этот член безразмерным. Эта константа необходима, когда D ≠ 4.

Может ли релятивистская струна быть заряжена? Выше приведенный аргумент делает очевидным то, что Максвелловский заряд переносится точками. Замкнутые струны не имеют специальных точек, но открытые струны имеют особые точки - конечные точки струн. Поэтому, вполне вероятно, что концы открытых струн несут электрический Максвелловский заряд. Позже мы покажем, что это действительно так и происходит. Пока, однако, мы наблюдаем нечто совсем другое. Т.к. электрический Максвелловский заряд естественно ассоциируется с точками, мы хотели бы узнать, нет ли здесь зарядов нового типа, который естественно ассоциировался бы с струнами. Для нового типа заряда нам необходим новый тип калибровочного поля. Таким образом, мы можем спросить: есть ли такое поле в струнной теории, которое связано со струной также, как Максвелловское поле связано с частицей? Ответ - да. Это поле есть антисимметричный 2-тензор Калаби-Рамона B_μν(=-B_νμ). Это безмассовое поле, которое возникает в замкнутой струнной теории (см. Раздел 13.3 и Задачу 10.6).

Давайте сейчас повторим логические заключения, которые привели нас к (15.1). В любой точке струнной траектории мы имеем два линейно независимых касательных вектора. Действительно, с координатами мирового листа τ и σ два касательных вектора могут быть выбраны как ∂X^μ/∂τ и ∂X^μ/∂σ. С этими двумя касательными векторами и двух-индексным полем  B_μν можно сконструировать Лоренцовский скаляр:

                                                           (15.3)

Его можно себе представить, как взаимодействие струны с полем Калаби-Рамона. Оно называется электрическим взаимодействием, т.к. оно является естествкенным обобщением электрического взаимодействия точечной частицы с Максвелловским полем. Поэтому мы говорим, что струна несет электрический заряд Калаби-Рамона. Взаимодействие (15.3) должно быть безразмерным в естественных единицах, поэтому B_μν имеет единицы измерений, обратные квадрату длины, или квадрату массы: [B_μν] = M². Это взаимодействие должно быть также инвариантным при репараметризациях (τ,σ) в точности также, как струнное действие Намбу-Гото. Мы увидим в задаче 15.1, что антисимметрия B_μν необходима для гарантии репараметризационной инвариантности (15.3). Важное указание относительно степени сохранения репараметризационной ивариантности будет рассмотрено позже в этой секции.

В точности также, как (15.2) представляет полную динамику частицы и Максвелловского поля, струнное взаимодействие (15.3) должно быть дополнено струнным действием S_стр и членом, дающим динамику поля B_μν:

                       (15.4)

Здесь мы используем антисимметризацию

a^[μb^ν] ≡ a^μb^ν - a^νb^μ                                                                                            (15.5)

и определение напряжения поля H_μνρ, ассоциированное с B_μν:

H_μνρ ≡ ∂_μB_νρ + ∂_νB_ρμ + ∂_ρB_μν ,                                                                         (15.6)

как в задаче (10.6). В последнем члене с правой стороны (15.4) мы ввели размерную константу к, необходимую, чтобы сделать этот член безразмерным ([k²] = M^D-6). В теории замкнутой струны константа k зависит от струнного взаимодействия и α'. Антисимметризация отвечает за возникновение коэффициента 1/2, на который умножается второй член правой стороны в (15.4). Мы антисимметризовали коэффициент перед B_μν , т.к. это сделать естественно: т.к. B_μν антисимметричен, то любая симметричная часть коэффициента не дает вклада в произведение. Заметим гибридную природу действия (15.4): часть ее является интегралом по мировому листу струны, а часть - интегралом по всему пространству-времени.

Чтобы понять природу струнного заряда, мы рассмотрим урвнения Максвелла (3.33), где электрический ток появляется как источник электромагнитного поля:

                                                                                                 (15.7)

Здесь плотность электрического заряда j⁰. Статическая частица дает электрический заряд, но нулевой электрический ток. Частица есть источник электрического поля, а струна - источние поля B_μν. Есть уравнение движения для поля B_μν, аналогичное (15.7). Мы поолучим это уравнение вычисляя вариацию действия (15.4) при вариациях δ B_μν(x). Вариация последнего члена в действии была вычислена в Задаче 10.6:

                                           (15.8)

Чтобы варьировать второй член в S, мы должны варьировать B_μν(x), но в этом члене поле вычисляется на мировом листе струны. Поле B_μν(x) может быть перезаписано как интеграл по всему пространству-времени от B_μν(x), умноженному на дельта-функцию, которая локализует поле на мировой лист:

                                                      (15.9)

С этим выражением второй член в S записывается как

,              (15.10)

где мы уже ввели символ j^μν со значением

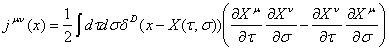                                 (15.11)

Заслуживает внимания замечание о том, что j^μν поддерживается (т.е. не исчезает) только на пространственно-временных точках, принадлежащих мировому листу струны. Действительно, если х не лежит на мировом листе,то аргумент дельта-функции никогда не равен нулю и интеграл исчезает. Объект j^μν играет роль тока. Из его конструкции следует, что он является антисимметричным при перестановке его индексов:

j^μν = - j^μν .                                                                                                (15.12)

Мы уже сделали всю работу, необходимую для нахождения уравнения движения для В_μν.Комбинируя уравнения (15.8) и (15.10), получаем общую вариацию действия S, как:

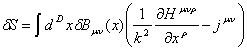.                                                              (15.13)

Если эта вариация равна нулю для произвольной, но антисимметричной δB_μν, антисимметричная часть коэффициента, умножающего δB_μν, должна быть равной нулю (задача 15.2). Т.к. полный член в скобках антисимметричен, то он должен быть равен нулю:

.                                                                                          (15.14)

Быстрое вычисление 15.1       пропущено

Подобие между (15.14) и (15.7) замечательное. Оно предполагает, что j^μν такого же типа, как сохраняемый ток. Вектор j^μ с правой стороны (15.7) является сохраняемым током, потому что

,                                                                                       (15.15)

в согласии с антисимметричностью F^μν и симметрией при перестановке частных производных.

С помощью тех же рассуждений из уравнения (15.14) получаем:

.                                                                                  (15.16)

Индекс μ в j^μν связан в уравнении сохранения, а индекс ν - свободен. Таким образом, тензор j^μν может рассматриваться как набор токов, помеченных индексом ν. Для каждого фиксированного ν компоненты тока заданы различными значениями μ. Т.к. нулевой компонент тока есть плотность заряда, мы имеем несколько зарядовых плотностей j^0ν. Точнее, т.к. j⁰⁰ = 0 (15.12), не исчезающие зарядовые плотности есть j^0kс k, пробегающим пространственные значения. Поэтому зарядовые плотности струны определяют пространственный вектор:

Плотность заряда Калаби-Рамона есть вектор j̃⁰ с компонентами j^0k.           (15.17)

Мы скоро докажем, что вектор плотности заряда является касательным к струне. Рассмотрим уравнение (15.16) для ν = 0:

                                                                                          (15.18)

Это утверждает, что плотность заряда струны есть бездивергентный вектор:

                                                                                                   (15.19)

Векторный заряд струны Q̃ естественно определен как пространственный интеграл плотности заряда струны:

                                                                                                 (15.20)

Чтобы подробнее разобраться в понятии струнного заряда, давайте вычислим j^μν в статической калибровке X⁰ = τ. При этом условии дельта-функция в уравнении (15.11) принимает форму

                                       (15.21)

и мы можем выполнить интегрирование по τ, чтобы найти

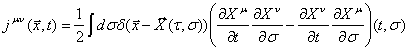                               (15.22)

Ясно, что при любои фиксированном времени t₀ ток j^μν, не исчезает на струне - множестве точек Для j^0k второй член в (15.22) не дает вклада согласно тому, что X⁰ = t, и мы находим, что

                                                              (15.23)

Коэффициент X̃' с правой стороны этого уравнения говорит нам, что в каждой точке на струне струнная плотность заряда j̃⁰ касательна к струне. Она указывает фактически направление вдоль касательной в сторону увеличения σ. Т.к. ориентация струны, как принято, - явл. направлением увеличения σ, то вектор плотности заряда лежит вдоль ориентации струны!

Это может показаться загадкой. Мы уже подчеркивали,что репараметризационная инвариантность действия струны означает, что изменение параметризации не может изменить физику. Изменение направления увеличения σ является репареметризацией, поэтому как оно может изменить плотность струнного заряда? В то время, как действие Намбу-Гото инвариантно при любой репараметризации, взаимодействие (15.3) струны с полем Калаби-Рамона - нет. Если мы сделаем замену σ→π - σ, поддерживая τ инвариантным, мера dτdσ не изменяет знак, но X^ν' изменяет знак. В результате, (15.3) изменяет знак. В действительности любая репараметризация, которая изменяет ориентацию мирового листа, будет реверсировать знак этого члена (задача 15.1).

Поэтому открытые струны являются ориентируемыми кривыми. В любое фиксированное время они полностью определены кривой в пространстве вместе с идентификацией конечной точки, которой соответствует σ = 0 (или, эквивалентно, конечной точки с σ = π). Хотя замкнутые струны не имеют конечных точек, они еще имеют ориентацию, которая также определена направлением увеличивающегося σ. Теории открытой и замкнутой струны, которые мы изучали в предыдущих главах были теориями ориентированных открытых струн и ориентированных замкнутых струн, соответственно. Теории неориентированных струн существуют. Это последовательные теории, полученные обрезанием пространства состояний (ориентированных) струнных теорий до подпространства состояний, которые являются инвариантными при операциях реверсирования ориентаций. Мы изучали эти теории в серии задач, начинающихся с задачи 12.10 и 13.5. Теория неориентированных замкнутых струн не имеет в своем спектре поля Калаби-Рамона. Это хорошо соответсвует нашему обсуждению состояний неориентированных струн, которые не несут струнный заряд (что указывает на это?).

Интеграл в (15.23) легко вычисляется для бесконечно длинной статической струны, расположенной вдоль оси х¹ (подобная конфигурация была изучена в секции 6.7). Эта струна описана уравнениями

X¹(t,σ) = f(σ), X² = X³ = ... = X^d = 0,                                                             (15.24)

где f(σ) - функция от σ, чья область изменений находится в интервале от -∞ до +∞. Функция f должна быть либо строго возрастающей, либо строго убывающей функцией от σ. Мы ожидаем, что это различие является значимым, т.к. эти две альтернативы соответствуют струнам с противоположными ориентациями. Только Х¹ имеет зависимость от σ, поэтому уравнение (15.23) приводит к тому, что единственная неисчезающая компонента j^μν есть j⁰¹ (= - j¹⁰):

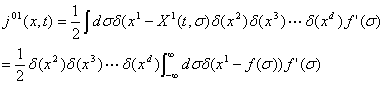                                    (15.25)

Пусть σ(х¹) означает уникальное решение уравнения  х¹ - f(σ) = 0, известное свойство дельта-функции дает

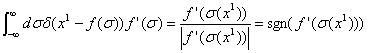                                     (15.26)

где sgn(a) означает знак a. Т.к. функция f является строго возрастающей или строго убывающей, то этот знак либо положителен, либо отрицателен по всему х¹. Таким образом, возвращаясь к j⁰¹(x̃, t), получаем:

j⁰¹(x¹, ..., x^d;t) = 1/2 sgn(f ')δ(x²)... δ(x^d) = 1/2 sgn(f ') δ(x̃_┴),                               (15.27)

где x̃_┴ есть вектор, чьи компоненты содержат направления, ортогональные к струне. Плотность заряда струны локализована на струне и мы явно видим зависимость ориентации от знака f '. Для произвольной статической струны пространтвенные координаты струны Х^к не зависят от времени. В результате, уравнение (15.22) дает:

j^ik= 0 для статической струны.                                                                    (15.28)

Для статической струны не пропадает только плотность заряда струны j^0k.

Перед завершением этой секции давайте коротко обсудим происхождение фоновых полей. Мы уже аргументировали то, что струнное действие должно быть пополнено взаимодействием (15.3). Вы можете спросить: не ошиблись мы в нашем прежнем квантовании струны, когда мы не рассматривали этот дополнительный член в струнном действии? Нет, наше квантование было правильно для нулевого фонового поля Калаби-Рамона. Поле B_μν в (15.3) называется фоновым полем Калаби-Рамона. Фоновое поле Калаби-Рамона - есть поле B_μν , которое удовлетворяет своим классическим уравнениям движения. Логический процесс, который привел нас к рассмотрению фоновых полей - следующий. Мы квантовали замкнутую струну и открыли Калаби-Рамона - состояния частицы. Из этих квантовых состояний мы вывели существование полей B_μν и получили их (линеаризованные) уравнения движения. Постулируя, что фоновые поля существуют, мы заключили, что есть нетривиальные поля B_μν, которые удовлетворяют своим полным уравнениям движения. Когда говорят о фоновых электромагнитных полях, имеют ввиду поля Е̃ и В̃, которые удовлетворяют уравнениям Максвелла. Аналогично, гравитационный фоновое поле есть пространство-время, чья метрика g_μν удовлетворяет уравнениям Эйнштейна общей теории относительности.

Допустим, задана некоторая конфигурация поля  B_μν. Как определить, может ли она быть фоновым полем? Если мы знаем полный набор нелинейных полевых уравнений, мы можем просто проверить, является ли эта конфигурация поля решением этих уравнений. Так как мы не знаем таких полевых уравнений, то необходима менее прямая процедура. Мы должны вновь проквантовать струну, на этот раз используя взаимодействие (15.3), чтобы проверить согласие с эффектами кандидата на фоновое поле  B_μν. Если квантование является успешным, то мы можем заключить, что эта конфигурация поля обеспечивает фон. Эта процедура может быть проведена на практике и физики уже открыли некоторые фоновые поля B_μν.

 

Вернуться к оглавлению